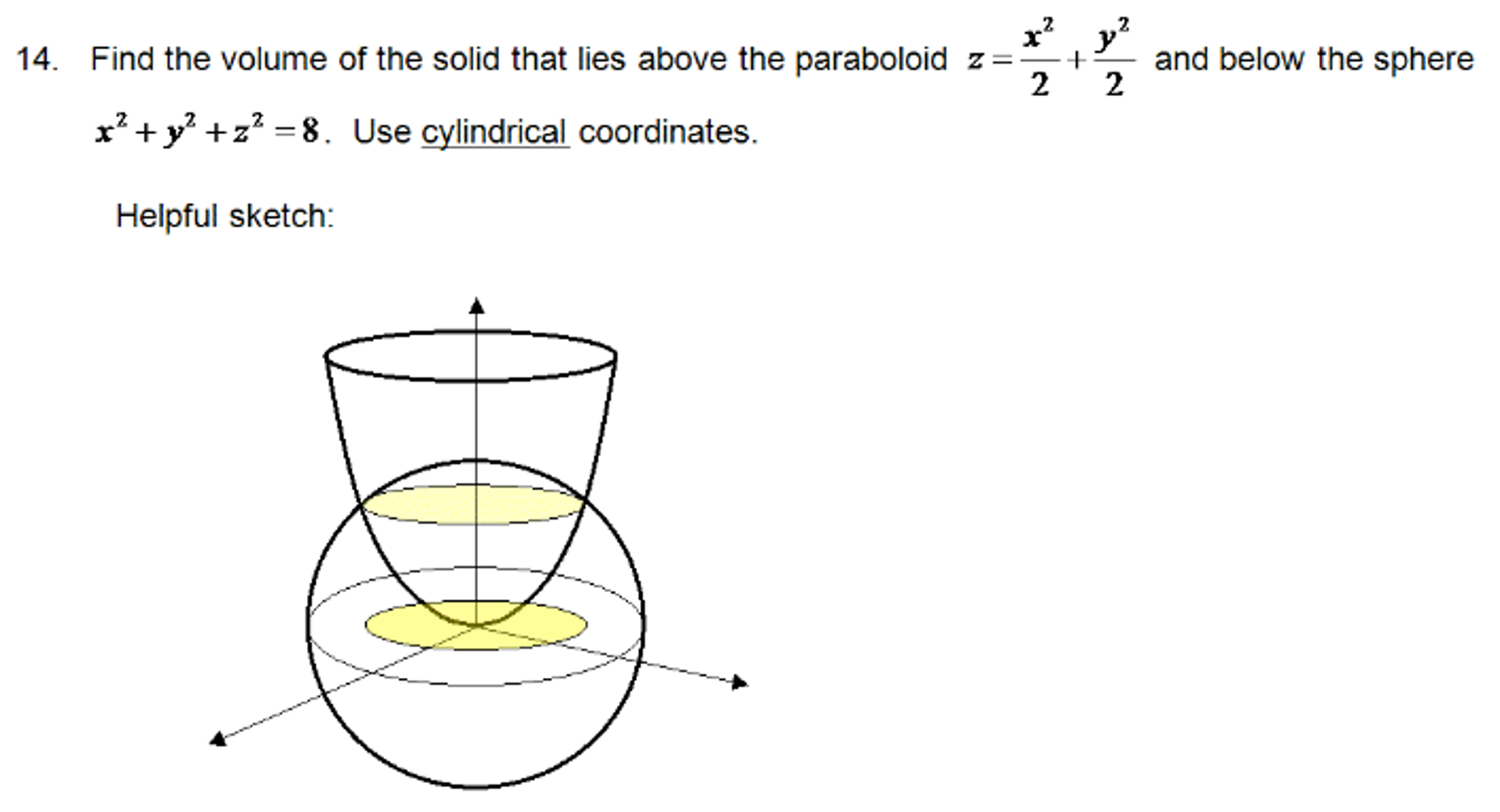
How would z = y 2 x 2 look different than z = x 2 y 2?Find the volume of the solid above the paraboloid z = x^2 y^2 and below the halfcone z = square root x^2 y^2 Question Find the volume of the solid above the paraboloid z = x^2 y^2 and below the halfcone z = square root x^2 y^2The given expression for below the half cone is z =√(x2y2) z = ( x 2 y 2) Solve the equation for a paraboloid z = (x2 y2) z = ( x 2 y 2) Suppose x = rcosθ x = r cos θ and y

Find The Volume Of The Solid That Lies Between The Chegg Com
Paraboloid z=1-x^2-y^2
Paraboloid z=1-x^2-y^2-Z= r 2and the paraboloid z= 3x 3y2;The area of a surface of the form math\displaystyle z=f(x,y)=x^{2}y^{2}/math is the double integral math\displaystyle\iint_R\sqrt{1(\frac{\partial f}{\partial



Find The Volume Of The Solid That Lies Above The Chegg Com
The plane x y 2 z = 2 intersects the paraboloid z = x 2 y 2 in an ellipse Find the points on this ellipse that are nearest to and farthest from the originUse cylindrical coordinates Evaluate $ \iiint_E z\ dV $, where $ E $ is enclosed by the paraboloid $ z = x^2 y^2 $ and the plane $ z = 4 $Find the volume of the solid that lies between the paraboloid z = x2 y2 and the sphere x2 y2 z2 = 2 using 1 (15%) the cylindrical coordinate, and 2 (15%) the spherical coordinate Sol First we nd the intersection of the paraboloid and the sphere If (x,y,z) is on the intersection,
2Find the volume of the solid under the paraboloid z= x2 y2 and above the disk x2 y2 9 3 Pencil problem Find the volume of the solid inside the cylinder x2 y2 = 4 and between the cone z= 5 p x2 y2 and the xyplane 4 Ice cream problem Find the volume of the solid above the cone z= p x2 y2 and below the paraboloid z= 2 x2 y2 5Figure 1 Region S bounded above by paraboloid z = 8−x2−y2 and below by paraboloid z = x2y2 Surfaces intersect on the curve x2 y2 = 4 = z So boundary of the projected region R in the x−y plane is x2 y2 = 4 Where the two surfaces intersect z = x2 y2 = 8 − x2 − y2 So, 2x2 2y2 = 8 or x2 y2 = 4 = z, this is the curve atConsider the paraboloid z = x2 y2 (a) Compute equations for the traces in the z = 0, z = 1, z = 2, and z = 3 planes Plane Trace z = 0 Point (0;0) z = 1 Circle x 2 y = 1 z = 2 Circle x 2 y = 2 z = 3 Circle x2 y2 = 3 (b) Sketch all the traces that you found in part (a) on the same coordinate axes
A paraboloid described by z = x ^ 2 y ^ 2 on the xy plane and partly inside the cylinder x ^ 2 y ^ 2 = 2y How do I find the volume bounded by the surface, the plane z = 0, and the cylinder?1 Let Ube the solid enclosed by the paraboloids z= x2 y2 and z= 8 (x2 y2) (Note The paraboloids intersect where z= 4) Write ZZZ U xyzdV as an iterated integral in cylindrical coordinates x y z Solution This is the same problem as #3 on the worksheet \Triple Integrals", except that we are now given a speci c integrandFor example, can be parametrized by x= rcos ;y= rsin ;z= 3r2 • The cone z= p x2 y2 has a parametric representation by x= rcos ;y= rsin ;z= r The cone z= 5 2 p x2 y2;for example, has parametric representation by x= rcos ;



Hyperbolic Paraboloid Saddle Z X 2 Y 2 Download Scientific Diagram



Surfaces
The paraboloid is the zero level set of the function f (x, y, z) = x 2 y 2 − z Its gradient is ∇f (x, y, z) = 2xi 2yj − k ∇f (1, 1, 2) = 2i 2j − k The normal line can be parametrized by σ(t) = (1 2t, 1 2t, 2 − t) It intersect the paraboloid, when f (σ(t)) = 0, meaning that t satisfies (1 2t) 2 (1 2t 2) − (2 In converting the integral of a function in rectangular coordinates to a function in polar coordinates dx dy rarr (r) dr d theta If z = f(x,y) = x^2 y^2 then f_x' = 2x and f_y'= 2y The Surface area over the Region defined by x^2y^2 = 1is given by S =int int_R sqrt(4x^2 4y^2 1) dx dy Converting this to polar coordinates (because it is easier to work with the circular RegionVolume Of Paraboloid Z X 2 Y 2 vianocna pohladnica vianočný pozdrav bez textu veseleho silvestra obrazky na silvestra a novy rok veselé vianoce vianočné obrázky na stiahnutie zadarmo verne gyula utazás a föld középpontja fel




Find The Area Of The Surface That Is Part Of The Paraboloid Z X 2 Y 2 That Lies Inside The Cylinder X 2 Y 2 9 Sketch A Graph Study Com




Finding The Surface Area Of The Paraboloid Z 1 X 2 Y 2 That Lies Above The Plane Z 4 Mathematics Stack Exchange
Problems Flux Through a Paraboloid Consider the paraboloid z = x 2 y 2 Let S be the portion of this surface that lies below the plane z = 1 Let F = xi yj (1 − 2z)k Calculate the flux of F across S using the outward normal (the normal pointing away from the zaxis) Answer First, draw a picture The surface S is a bowl centered on the zaxisQuestion Find the Volume of the Solid that lies under the paraboloid z=x 2 y 2 above the XYplane, and inside the cylinder x 2 y 2 =2x check_circle2 Let F~(x;y;z) = h y;x;zi Let Sbe the part of the paraboloid z= 7 x2 4y2 that lies above the plane z= 3, oriented with upward pointing normals Use Stokes' Theorem to nd




Find An Equation For The Paraboloid Z 4 X 2 Y 2 In Cylindrical Coordinates Type Theta In Your Answer Study Com



Find The Surface Area Of The Part Of The Paraboloid Z 5 X 2 Y 2 That Lies Between The Planes Z 0 And Z 1 Mathematics Stack Exchange
Y= rsin ;z= 5 2r Stoke's Theorem S is the part of the paraboloid z=x^2y^2 that lies insided the parabaloid and cyli Watch later Share Copy link Info Shopping Tap to unmute If playback doesn't begin shortly132 13 MULTIPLE INTEGRALS Example Find the volume of the solid that lies under the paraboloid z = x2 y2, above the xyplane, and inside the cylinder x2 y2 = 2x Completing the square, (x 1)2 y2 = 1 is the shadow of the cylinder in the xyplane Changing to polar coordinates, the shadow of the cylinder is r2 = 2rcos or r = 2cos , so



Http Www Cis Umac Mo Fstitl Calculus12 13 Lecture 07a Pdf



Surface Area
See full lesson here https//wwwnumeradecom/questions/usecylindricalcoordinatesevaluateiiint_ezdvwhereeisenclosedbytheparaboloidzx2y2andExample Find the centroid of the solid above the paraboloid z = x2 y2 and below the plane z = 4 Soln The top surface of the solid is z = 4 and the bottom surface is z = x2 y2 over the region D defined in the xyplane by the intersection of the top and bottom surfaces 2 Figure 3 The intersection gives 4 = x2 y2 Therefore D is a diskIt follows that x2 y2 = ˆ2 sin2 ˚ If we de ne the angle to have the same meaning as in polar coordinates, then we have x= ˆsin˚cos ;




Elliptic Paraboloid X 2 Y 2 Z 2 0 Download Scientific Diagram



1
41 The plane x y 2z= 2 intersects the paraboloid z= x2 y2 in an ellipse Find the points on the ellipse that are nearest to and farthest from the origin42 0 2 442 0 2 42 0 2 442 0 2 442 0 2 42 0 2 4 Here, the two constraints are g(x;y;z) = x y 2z 2 and h(x;y;z) = x2 y2 z Any critical answered by Taniska (645k points) selected by Vikash Kumar Best answer Let A (3, –6, 4) and let P (x, y, z) be any point on the paraboloid x2 y2 – z = 0 AP2 = (x – 3)2 ( y 6)2 (z – 4)2 by distance formulaQuora Functions (mathematics) Calculus Algebra Mathematics




Find The Volume Of The Solid Bounded By The Paraboloid Z X 2 Y 2 And The Plane Z 9 In Rectangular Coordinates Study Com




Hyperbolic Paraboloid Surface Z Y 2 X 2 Download Scientific Diagram
Of the paraboloid z = x2 y2 and a portion of the plane z = 4 Solution Let S 1 be the part of the paraboloid z = x 2 y 2 that lies below the plane z = 4, and let S 2 be the disk x 2 y 2 ≤ 4, z = 4Answer to Find the volume of the region D bounded above by the sphere x^2 y^2 z^2 = 128 and below by the paraboloid 8z = x^2 y^2 By signing Find the area of the part of the paraboloid z = x^2 y^2 that lies under the plane z = 25 The plane intersects the paraboloid in the circle x^2 y^2 = 25, z = 25 Therefore the given surface lies above the disk D with center the origin and radius 5 (See the figure) Using this formula, we have A = doubleintegral_D squareroot 1 (partial differential z/partial differential




Consider The Surface S That Consists Of The Part Of Chegg Com



Solved Find The Surface Area Of The Part Of The P
The hyperbolic paraboloid Equation z = A x 2 B y 2 (where A and B have DIFFERENT signs) With just the flip of a sign, say x 2 y 2 to x 2 − y 2, we can change from an elliptic paraboloid to a much more complex surface Because it's such a neat surface, with a fairly simple equation, we use it over and over in examplesParaboloid z = x2 y2 and below the half cone z = p x2 y2 Solution x = rcosθ, y = rsinθ, z = z, dV = rdrdθdz ZZZ E z dV = Z2π 0 Z1 0 Zr r2 zrdzdrdθ = Z2π 0 Z1 0 z2r 2 z=r z=r2 drdθ = Z2π 0 Z1 0 r3 2 − r5 2 drdθ = Z2π 0 r4 8 − r6 12 r=1 r=0 dθ = Z2π 0 1 24 dθ = π 12 Problem 5 Evaluate RRR E y dV, where E is enclosed by theThe plane x y 2z = 30 intersects the paraboloid z = x^2 y^2 in an ellipse Find the points on the ellipse that are nearest to and farthest from the origin




Find The Surface Area Of The Part Of The Circular Paraboloid Z X 2 Y 2 That Lies Inside The Cylinder X 2 Y 2 4 Study Com



Math 2 Midterm 2
Y= ˆsin˚sin We de ne the spherical coordinates of (x;y;z) to be (ˆ;C ={(x,y,z) x2 y2 =9, z =0} OrientSwith the upwardpointing unit normal vector n (See Figure 731) We verify StokesÕs theorem for the vector Þeld F=(2z y)i(x z)j(3x 2y)k y x z n S C = S Figure 731 The paraboloid z = 9 x2 y2 oriented with upward normaln Note that the boundary circle C is oriented consistently withS We calculate ו The paraboloid z = x2 y2 can be parametrized by x= rcos ;y= rsin ;




Find The Surface Area Of The Part Of The Paraboloid Z Chegg Com




Part Of The Elliptic Paraboloid Z X2 Y2 Which Can Be Generated By Rotating The Parabola Z X2 Or Z Y2 About The Z Axis Stock Photo Alamy
If you hear somebody refer simply to a "paraboloid," they generally mean an elliptic paraboloid, or even a surface where A=0 or B=0 If you're in doubt which surface somebody means, askFind the surface area of the part of the 2 z=x^(2)y^(2) paraboloid outside the cone z=sqrt(x^(2)y^(2)) Math Calculus MATH 0102 Comments (0) Answer & Explanation Unlock full access to Course Hero Explore over 16 million stepbystep answers from our library Get answer4) to spherical coordinates, we rst compute ˆ= p x2 y2 z2 = q 12 ( 3)2 ( 4)2 = = 2 5




1 Paraboloid Surface Z F X Y 0 5x 2 0 5y 2 Download Scientific Diagram




Stoke S Theorem S Is The Part Of The Paraboloid Z X 2 Y 2 That Lies Insided The Parabaloid And Cyli Youtube
The cross sections on the left are for the simplest possible elliptic paraboloid z = x2 y2 One important feature of the vertical cross sections is that the parabolas all open in the same direction That isn't true for hyperbolic paraboloids!Math 9 Assignment 5 Solutions 3 8 Find the surface area of the paraboloid z = 4 x2 y2 that lies above the xyplane Solution For this problem polar coordinates are useful S = ZZ, y = 2 1−λ, z = 10− λ 2 Substituting in the first equation and simplifying we get λ3 −22λ2 41λ−10 = 0 The exact expressions for the roots of this equation are too complicated The approximations for the roots are λ1 ≈, λ2 ≈174, λ3 ≈ The corresponding points on the paraboloid
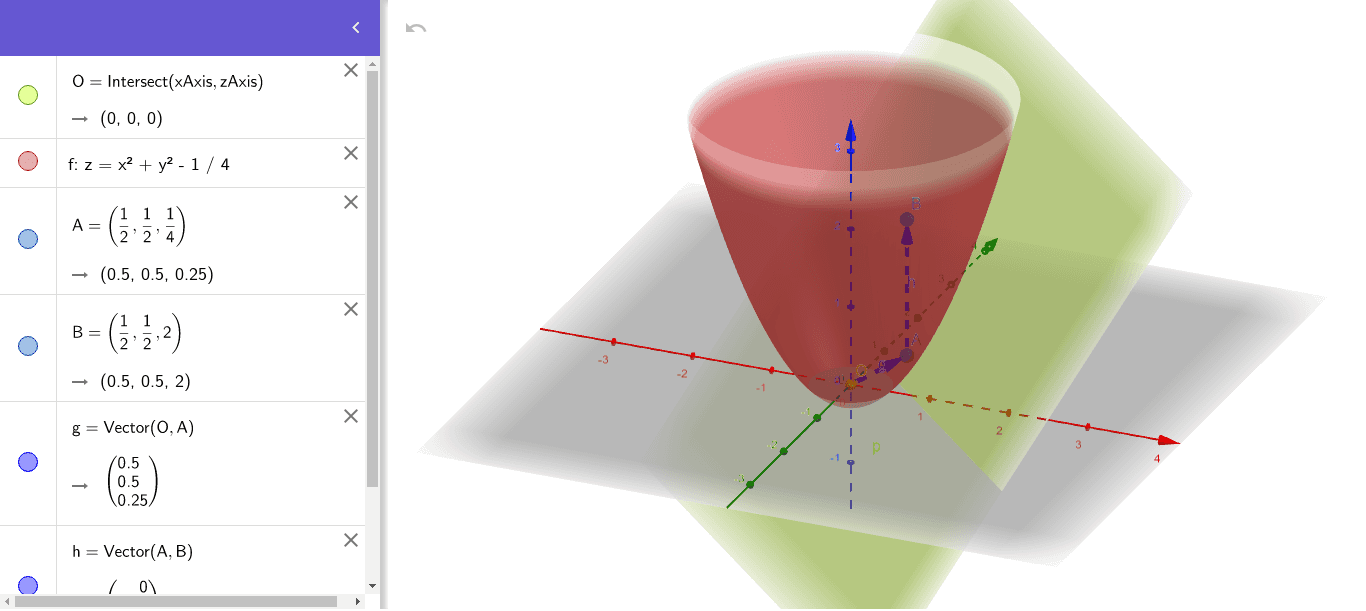



Paraboloid Geogebra



Surfaces Part 4
3 EX 1 Verify Stokes's Theorem for ˆ F = y2i xj 5zk if S is the paraboloid z = x2 y2 with the circle x2 y2 = 1 as its boundary ˆ ˆ x y z ⇀Compute answers using Wolfram's breakthrough technology & knowledgebase, relied on by millions of students & professionals For math, science, nutrition, history, geography, engineering, mathematics, linguistics, sports, finance, music WolframAlpha brings expertlevel knowledge and;˚) Example To convert the point (x;y;z) = (1;



What Is The Volume Between Paraboloid Z X 2 Y 2 And Y X 2 Z 2 Quora
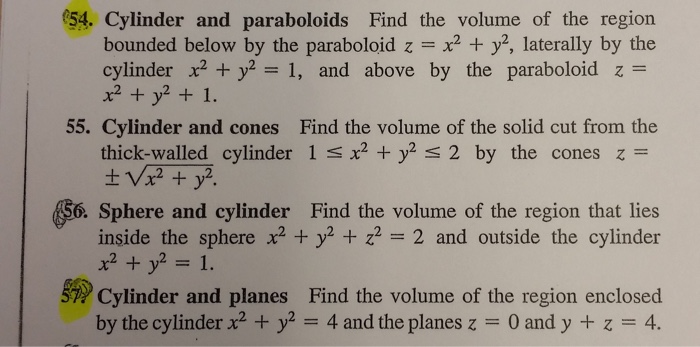



Cylinder And Paraboloids Find The Volume Of The Chegg Com
Engineering in your pocket Now study onthego Find useful content for your engineering study here Questions, answers, tags All in one app!The basic elliptic paraboloid is given by the equation z =Ax2By2 z = A x 2 B y 2 where A A and B B have the same sign This is probably the simplest of all the quadric surfaces, and it's often the first one shown in class It has a distinctive "nosecone" appearance



Http Math Colorado Edu Liuf Activecalc3 Quadricsurfacesmatching Pdf
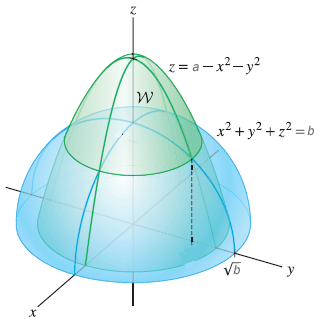



Let W Be The Region Above The Sphere X2 Y2 Z2 Chegg Com
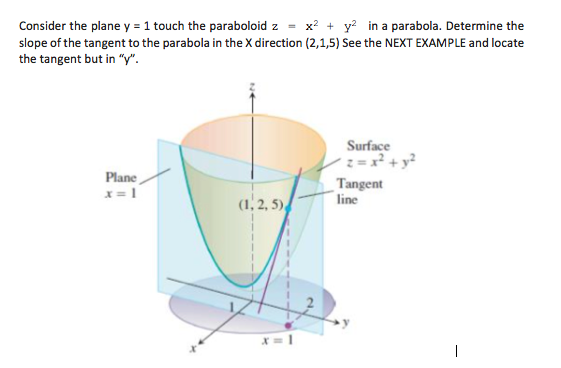



Consider The Plane Y 1 Touch The Paraboloid Z X2 Chegg Com
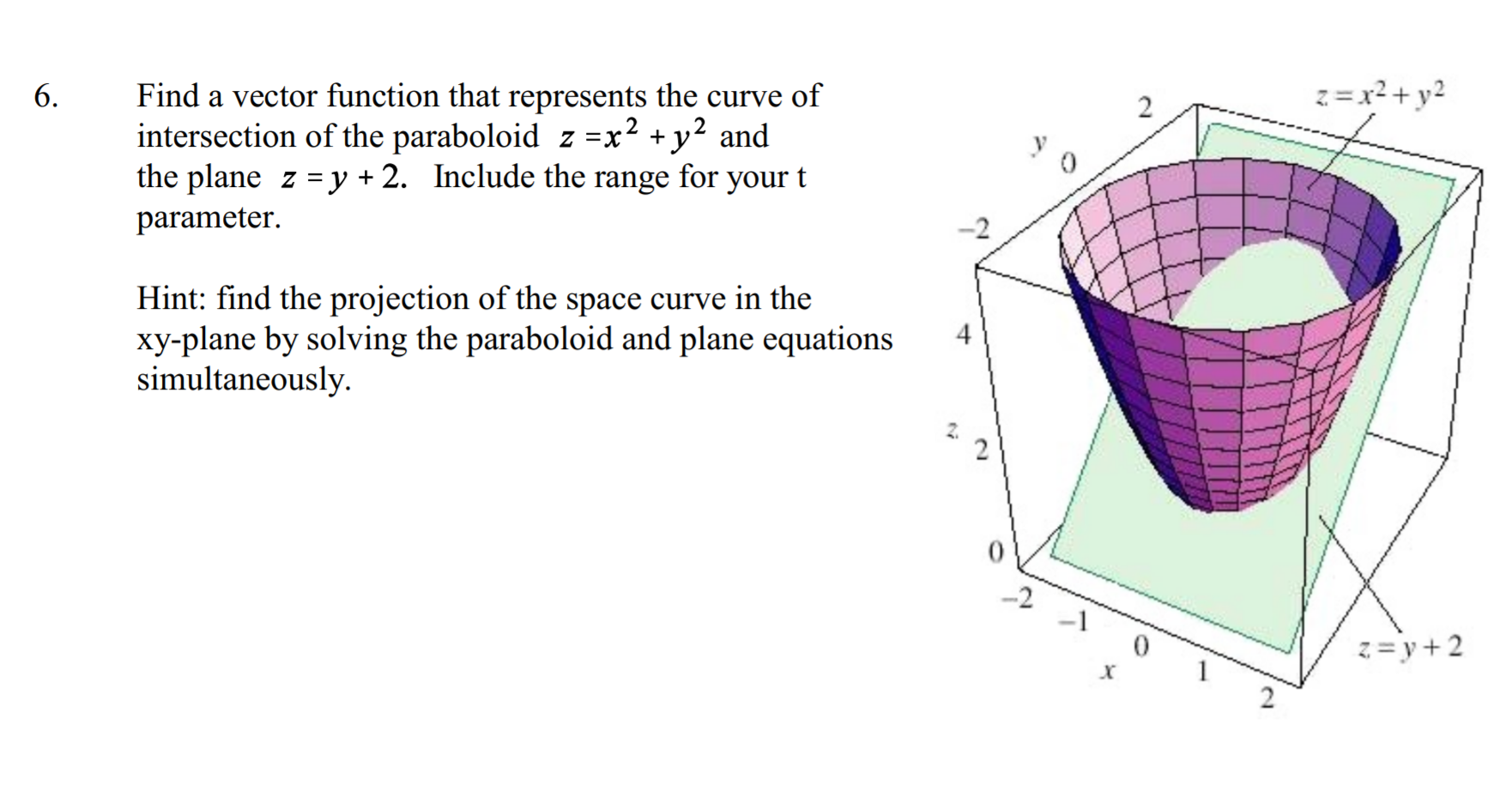



6 Z X2 Y2 2 Find A Vector Function That Represents Chegg Com




Consider The Paraboloid Z X 2 Y 2 The Plane 7x 8y Z 5 0 Cuts The Paraboloid Its Intersection Being A Curve Find The Natural Parametrization Of This Curve Hint The Curve Which Is Cut Lies Above Study Com




S Consists Of The Paraboloid Y X 2 Z 2 0 Y 1 And The Disk X 2 Z 2 1 Youtube



Elliptic Paraboloid Students Britannica Kids Homework Help
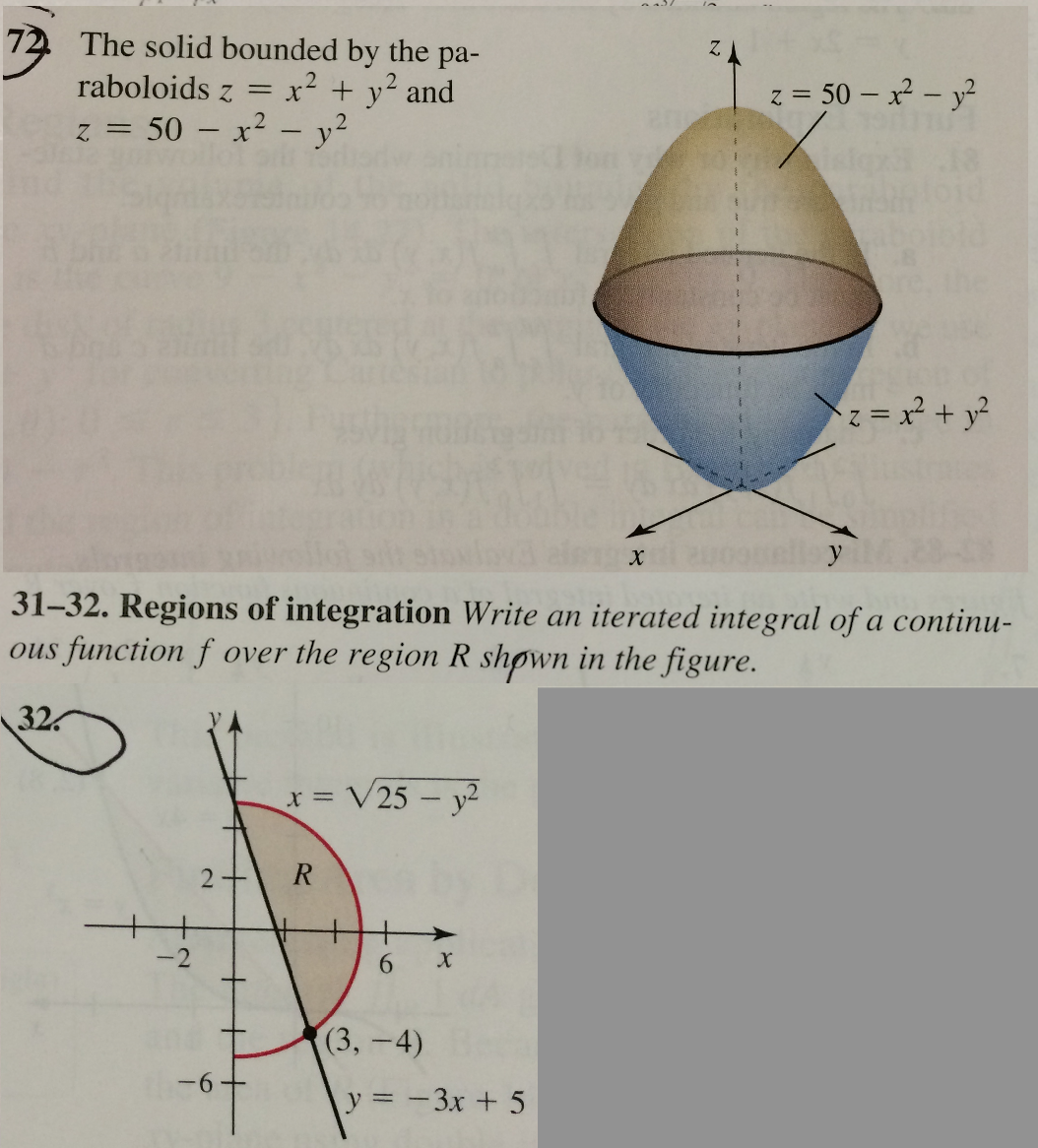



The Solid Bounded By The Paraboloids Z X 2 Y 2 Chegg Com




The Plane X Y 2z 12 Intersects The Paraboloid Z X2 Y2 In An Ellipse Find The Points On The Ellipse That Are Nearest To And Farthest From The Origin Wegglab



Solved Find The Volume Of The Given Solid Enclos
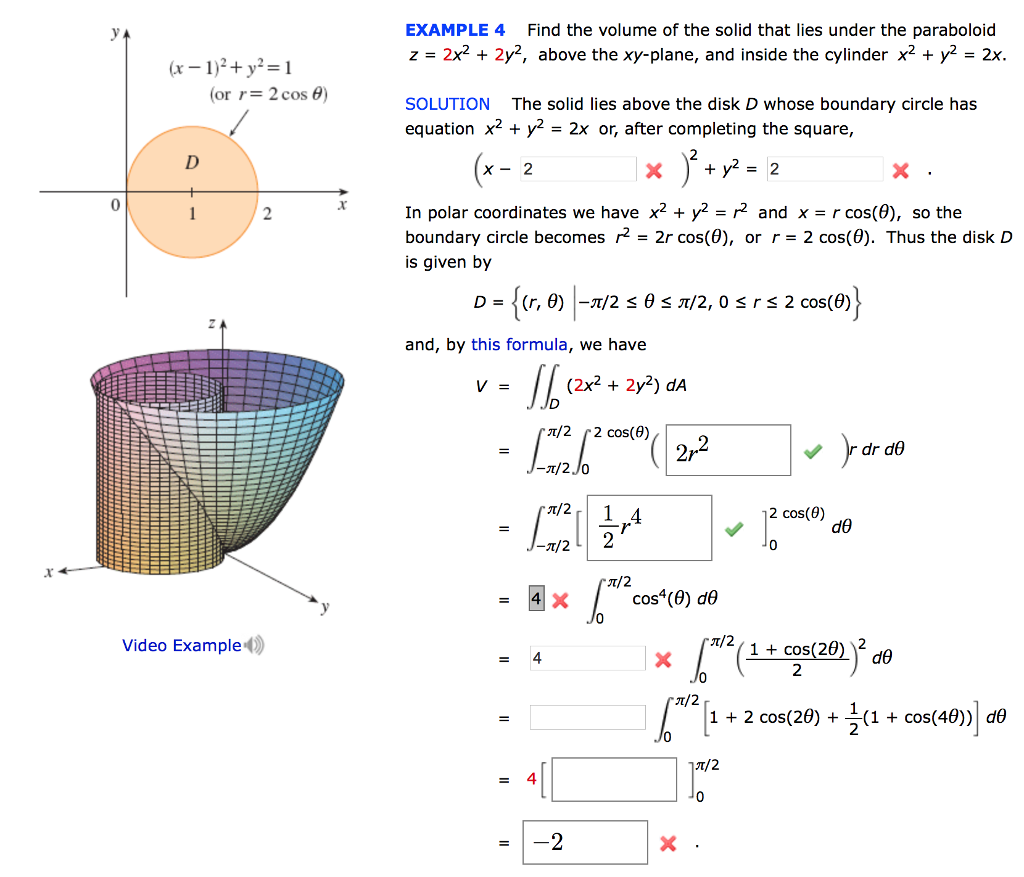



Example 4 Find The Volume Of The Solid That Lies Chegg Com




Use A Triple Integral To Find The Volume Of The Solid E Enclosed By The Paraboloid Z X 2 Y 2 And The Plane Z 16 Study Com



Http Www Mat Ucm Es Mpuente Docs Conicas Cuadricas 4 Quadric Surfaces Pdf




Use The Cylindrical Coordinates To Find The Volume Of Chegg Com




Use Polar Coordinates To Find The Volume Of The Given Solid Below The Paraboloid Z 18 2x 2 2y 2 And Above The Xy Plane Homework Help And Answers Slader
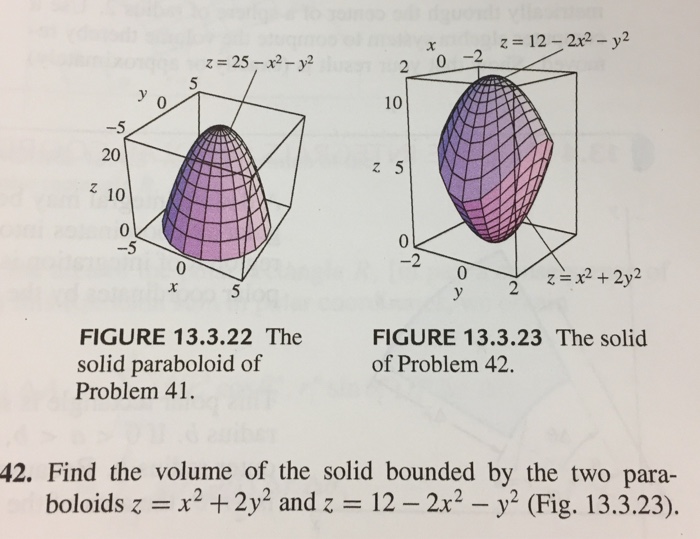



Find The Volume Of The Solid Bounded By The Two Chegg Com
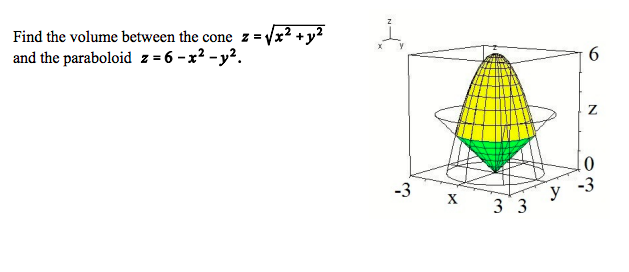



Find The Volume Between The Cone Z X2 Y2 And The Chegg Com




A Sketch And Identify The Surface Z X 2 Y 2 B Find The Equation Of The Intersection Z X 2 Y 2 With Z 5 Sketch And Identify It Study Com




4 5pts The Region Under The Surface Z X2 Y4 And Bounded By The Planes X 0 And Y 9 4 2 And Th Homeworklib




Parametric Surfaces We Can Use Parametric Equations To Describe A Curve Because A Curve Is One Dimensional We Only Need One Parameter If We Want To Ppt Download



What Is The Volume Bounded By The Paraboloid Math Z 2x 2 Y 2 Math And The Cylinder Math Z 4 Y 2 Math Quora




Calculus Volume Integral Mathematics Stack Exchange




Example 2 Find The Volume Of The Solid Bounded By The Chegg Com




Sketch A Graph Of The Paraboloid Z X 2 Y 2 Determine Whether The Outward Normal Vector N Should Point In The K Or K Direction And Calculate N In



Surfaces
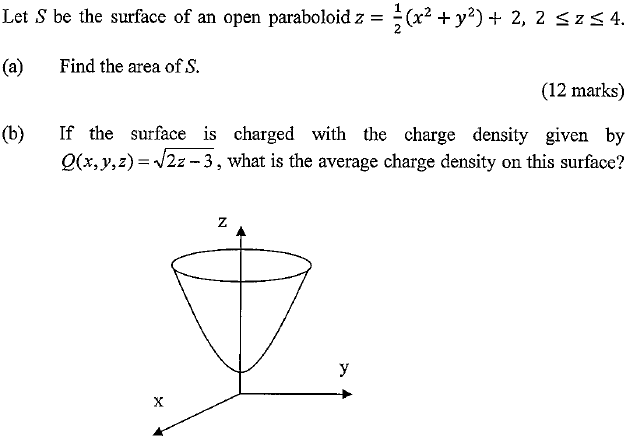



Let S Be The Surface Of An Open Paraboloid Z Chegg Com
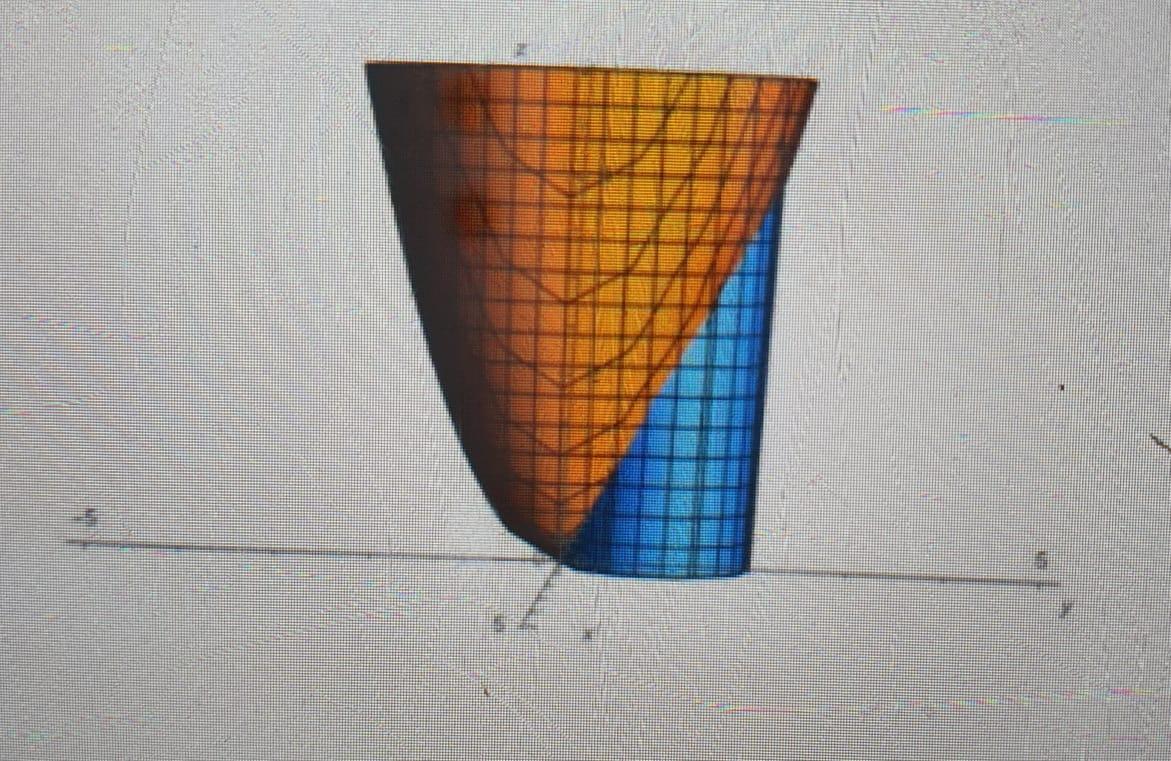



Solved Find The Volume Of The Solid That Lies Below The P Chegg Com




Find The Volume Of The Solid That Lies Above The Chegg Com



1




Consider The Intersection Of The Paraboloid Z X 2 Y 2 And The Plane Y X A Sketch The Paraboloid B Find The Parametrization Of The Curve Of Intersection Study Com




Use Cylindrical Coordinates To Set Up The Integral Chegg Com




A Hyperbolic Paraboloid Z X 2 Y 2 Download Scientific Diagram



1




Find The Volume Of The Solid That Lies Between The Chegg Com
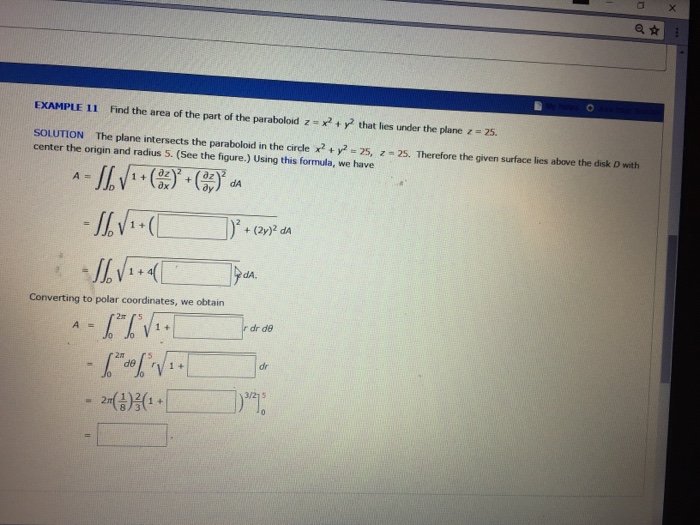



Find The Area Of The Part Of The Paraboloid Z X 2 Chegg Com




Find The Volume Of The Region Bounded By The Paraboloid Z 36 X 2 Y 2 And The Xy Plane Study Com




Surfaces Part 2




Finding The Surface Area Of The Paraboloid Z 1 X 2 Y 2 That Lies Above The Plane Z 4 Mathematics Stack Exchange




Example 4 Find The Volume Of The Solid That Lies Chegg Com




A Solid Is Bounded By The Paraboloid Z X 2 Y 2 The Cylinder X 2 Y 2 4 And The Xy Plane Use Cylindrical Coordinates To Find Its Volume And Its Centroid Study Com



Elementary Calculus Example 5 Same Of Hyperbolic Paraboloid



Part Of The Elliptic Paraboloid Z X2 Y2 Which Can Be Generated By Rotating The Parabola Z X2 Or Z Y2 About The Z Axis Stock Photo Alamy




5 Begin With The Paraboloid Z X2 Y2 For 0 Szs Chegg Com



Find An Equation For The Paraboloid Z X 2 Y 2 In Spherical Coordinates Enter Rho Phi And Theta For R ϕ And 8 Respectively Math Homework Answers




Multivariable Calculus Surface Area Of Sphere X 2 Y 2 Z 2 16z Within Paraboloid Z X 2 Y 2 Mathematics Stack Exchange



Answered 71 The Solid Bounded By The Paraboloid Bartleby




Find The Volume Of The Solid D Between The Paraboloids Z X 2 Y 2 And 12 2x 2 2y 2 Study Com




Find The Surface Area Of The Paraboloid Z 1 X 2 Y 2 That Lies Above The Unit Circle In The Xy Plane Study Com




Find The Volume Of The Solid That Lies Under The Chegg Com




Solved 21 The Solid Bounded By The Paraboloid Z 2 Y Chegg Com



Search Q Parabolic Cylinder Tbm Isch
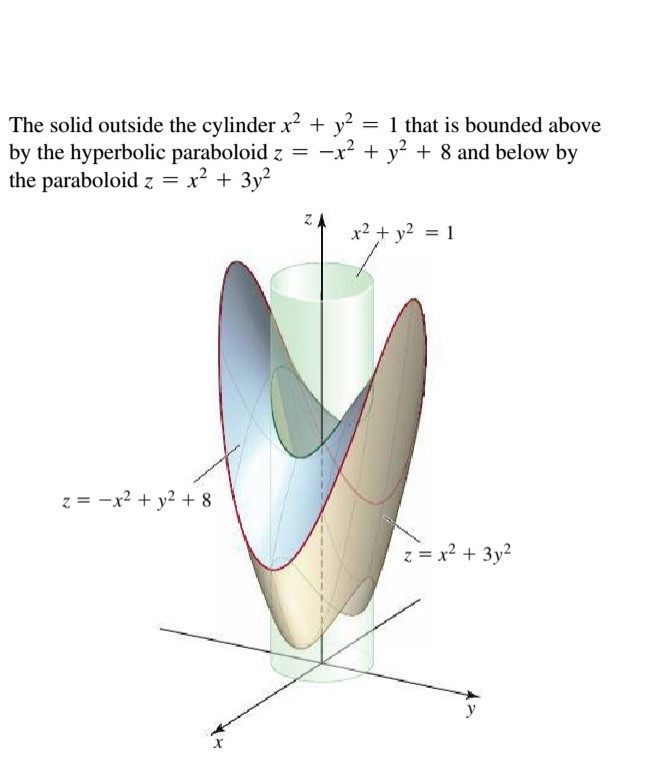



The Solid Outside The Cylinder X2 Y2 1 That Is Chegg Com



Http Math Colorado Edu Liuf Activecalc3 Quadricsurfacesmatching Pdf




Sketch The Solid Bounded By The Paraboloids Z 8 X 2 Y 2 And Z X 2 Y 2 Find The Volume Of The Solid Study Com




Find The Area Of The Paraboloid Z 1 X 2 Y 2 That Lies In The First Octant Study Com




Find The Volume Of The Solid Bounded By The Paraboloid Z X 2 Y 2 And The Plane Z 9 Study Com




Paraboloid Z 4 X 2 Y 2 Novocom Top




Elliptic Paraboloid X 2 Y 2 Z 2 0 Download Scientific Diagram




Find The Volume Of The Solid That Lies Between The Chegg Com



Http Www Mat Ucm Es Mpuente Docs Conicas Cuadricas 4 Quadric Surfaces Pdf
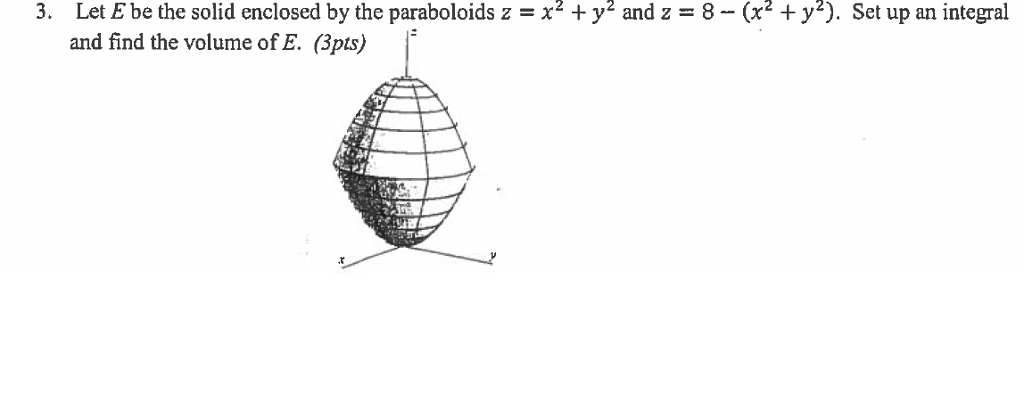



Let E Be The Solid Enclosed By The Paraboloids Z Chegg Com
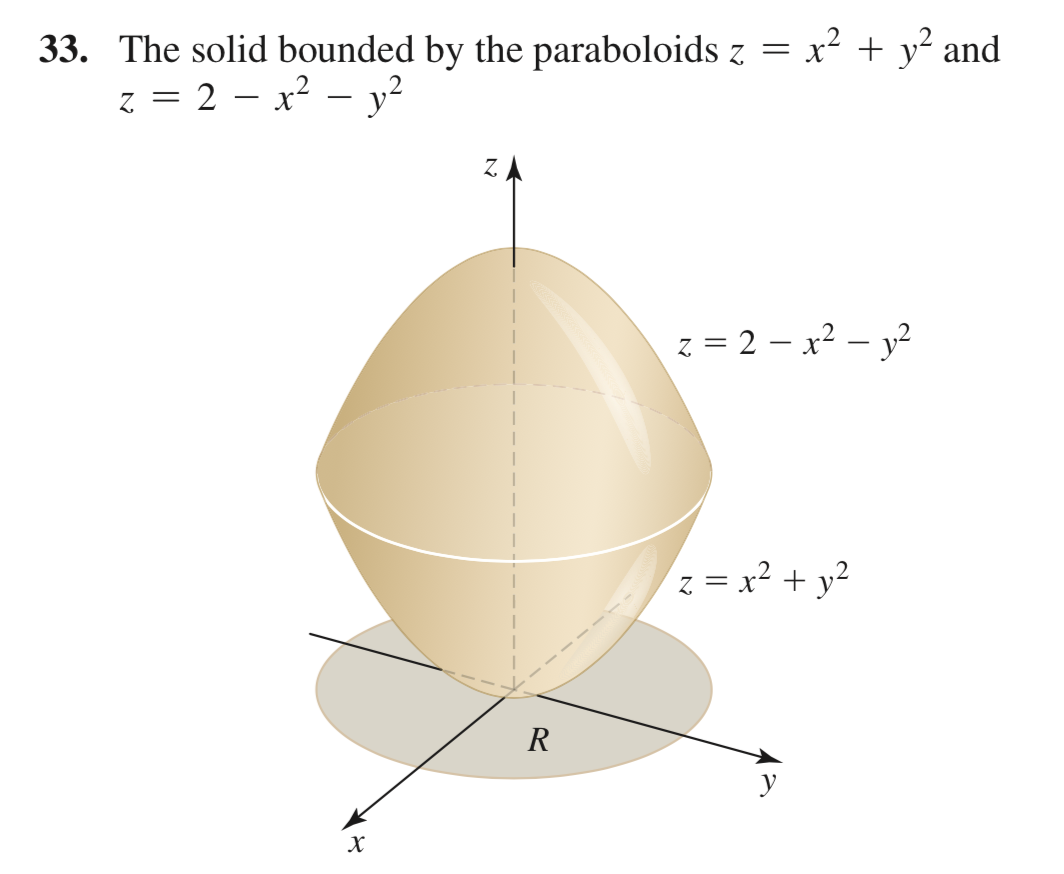



33 The Solid Bounded By The Paraboloids Z X2 Y2 Chegg Com




Hyperbolic Paraboloid X 2 1 M T X 2 2 Download Scientific Diagram




Calculus Integration Double Integrals 8 Of 9 Example 7 Finding The Volume Paraboloid Youtube




Find The Volume Of The Solid Bounded By The Plane Z Chegg Com



A Paraboloid Described By Z X 2 Y 2 On The Xy Plane And Partly Inside The Cylinder X 2 Y 2 2y How




The Paraboloid X 2 Y 2 16 Z Is Intersected By The Ellipsoid X 2 4 Download Scientific Diagram




Example 4 Find The Volume Of The Solid That Lies Chegg Com




3 A Consider The Standard Hyperbolic Paraboloid S Z Chegg Com




Find The Volume Of The Solid Bounded By The Plane Z 0 And The Paraboloid Z 1 X 2 Y 2 Use A Double Integral And Polar Coordinates Study Com




Let B Be The Solid Body Bounded By The Paraboloid Z Chegg Com




Paraboloid Z X 2 Y 2 Novocom Top




Example 11 Find The Area Of The Part Of The Chegg Com




The Solid Bounded By The Paraboloid Z 2 X 2 Y 2 Chegg Com




Draw The Solid Bounded By The Paraboloid Z 6 X 2 Y 2 And The Plane Z 0 Study Com




Analytical Representation Of Hyperbolic Paraboloid Z X 2 Y 2 For The Download Scientific Diagram
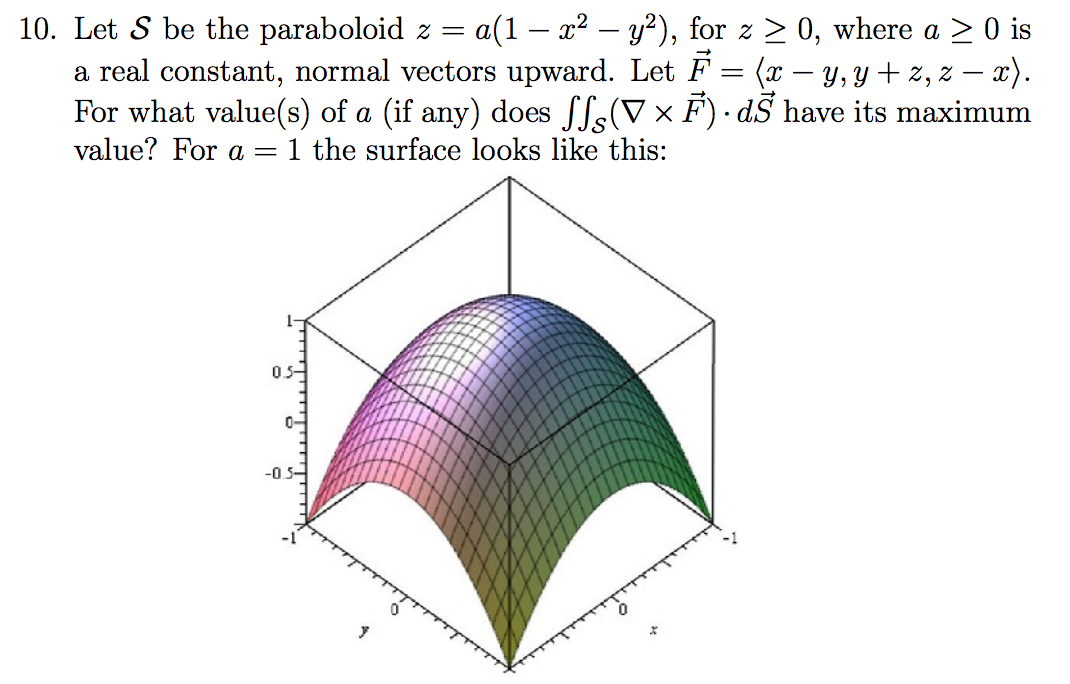



Let S Be The Paraboloid Z A 1 X 2 Y 2 For Z Chegg Com




Analytical Representation Of Hyperbolic 2 2 Paraboloid Z X Y For The Download Scientific Diagram




An Autoencoder Trained On A Paraboloid Z X 2 Y 2 Z 4 With The Download Scientific Diagram




Analytical Representation Of Hyperbolic Paraboloid Z X 2 Y 2 For The Download Scientific Diagram



0 件のコメント:
コメントを投稿